문제
2304번: 창고 다각형
첫 줄에는 기둥의 개수를 나타내는 정수 N이 주어진다. N은 1 이상 1,000 이하이다. 그 다음 N 개의 줄에는 각 줄에 각 기둥의 왼쪽 면의 위치를 나타내는 정수 L과 높이를 나타내는 정수 H가 한 개의
www.acmicpc.net
아이디어
첫번째 trial : 극댓값을 기준으로 설계 (엄청 공들여서 설계했는데, 틀렸었음 ㅠ)
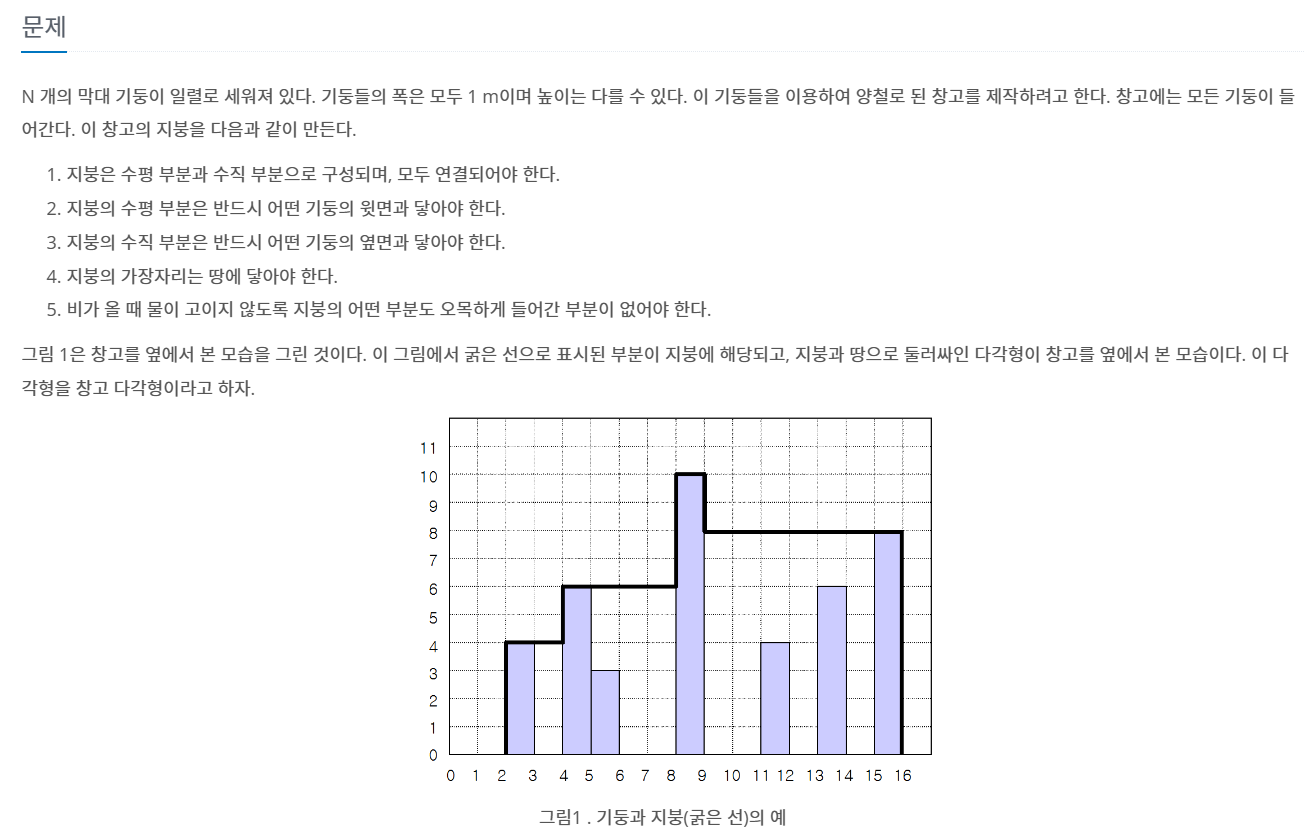
- 기둥들을 배열로 보면, 위 그림은 {4,0,6,3,0,0,10,0,0,4,0,6,0,8}이라 생각할 수 있다.
- 이때 기준이 되는 기둥들의 특징은 '기울기가 바뀌는 부분(=극댓값)'이라 생각함
- 따라서 극댓값에 해당하는 배열로 표시하고, 그 배열을 돌면서 너비를 구함
틀린 이유 : 극댓값으로 접근을 하는건 이 문제의 본질 파악하지 못한 것임
극댓값 양 옆에 더 큰 극댓값이 있다면, 이는 무시되기 때문 => 완전히 잘못 짚었다.

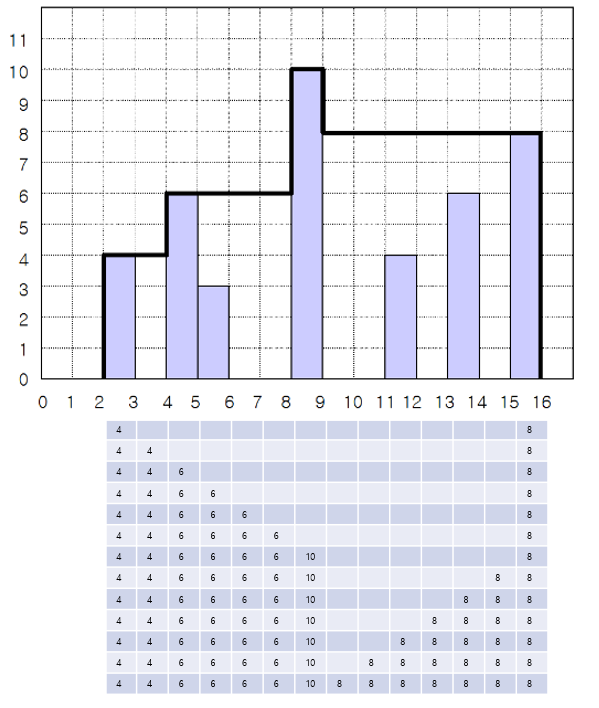
두번째 trial : 양끝에서 하나씩 이동하며 최댓값을 구하는 로직 구현
- 양끝의 최댓값을 비교하여, 더 작은 쪽을 한칸 움직인다.
양끝의 최댓값을 비교하는 이유는 양끝 값이 직접적으로 연관이 있어서가 아니라,
이렇게 하면 ① left와 right가 만났을 때, 만난 곳 전 후로 동일한 로직이 적용되었음이 보장된다.
② 따라서 max 이후에 완전히 새로운 로직을 짜야했던 순방향 로직보다 더 간단해진다. - 움직인 곳의 값이 기존 최댓값보다 작으면, 결과에 기존 최댓값을 더해준다.
- 움직인 곳의 값이 기존 최댓값보다 크면, 최댓값을 갱신하고 결과에 갱신된 최댓값을 더해준다.
코드
package javaPractice.BJ2304;
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 기둥 입력받기
int count = Integer.parseInt(br.readLine());
HashMap<Integer, Integer> hm = new HashMap<>();
for (int i = 0; i < count; i++) {
String[] sArr = br.readLine().split(" ");
hm.put(Integer.parseInt(sArr[0]), Integer.parseInt(sArr[1])); //(위치, 높이)
}
// 위치 순서대로 정렬하기
LinkedList<Integer> ll = new LinkedList(hm.keySet());
Collections.sort(ll);
int lIdx = ll.getFirst();
int rIdx = ll.getLast();
int lMax = hm.get(lIdx);
int rMax = hm.get(rIdx);
int sum = 0;
while(lIdx<=rIdx){
// 왼쪽 최대가 오른쪽 최대보다 크면, 오른쪽 max를 갱신하고 이동시키기
if(lMax>rMax){
rMax = Math.max(rMax, hm.getOrDefault(rIdx, rMax));
sum += rMax;
rIdx--;
} else {
lMax = Math.max(lMax, hm.getOrDefault(lIdx, lMax));
sum += lMax;
lIdx++;
}
}
System.out.println(sum);
}
}
알게된 것
배열에서 원하는 것을 탐색할 때 for문처럼 순차적으로 탐색하는 방법만 있는게 아니라,
양 끝에서 하나씩 옮기며 접근하는 while(left<right) 방법이 있다는 것을 생각도 하지 못했다. (그냥 생각 자체를 못함)
이 경우, 순차적 접근은 고려해야 할 것이 너무 많지만
양방향 접근은 동일한 로직을 적용할 수 있으므로 더 간단하다.
머릿속에 '양방향 접근(끝 값 비교)' 에 대한 선택지를 넣어두자!!
'Algorithm > 알고리즘 문제' 카테고리의 다른 글
| 백준 10434번 : 행복한 소수 (0) | 2023.07.12 |
|---|---|
| 백준 2992번 : 크면서 작은 수 (0) | 2023.07.12 |
| 백준 5397번 : 키로거 (0) | 2023.06.25 |
| 백준 1406번 : 에디터 (0) | 2023.06.24 |
| 백준 2608번 : 로마 숫자 (0) | 2023.06.23 |


