컬렉션으로서의 큐
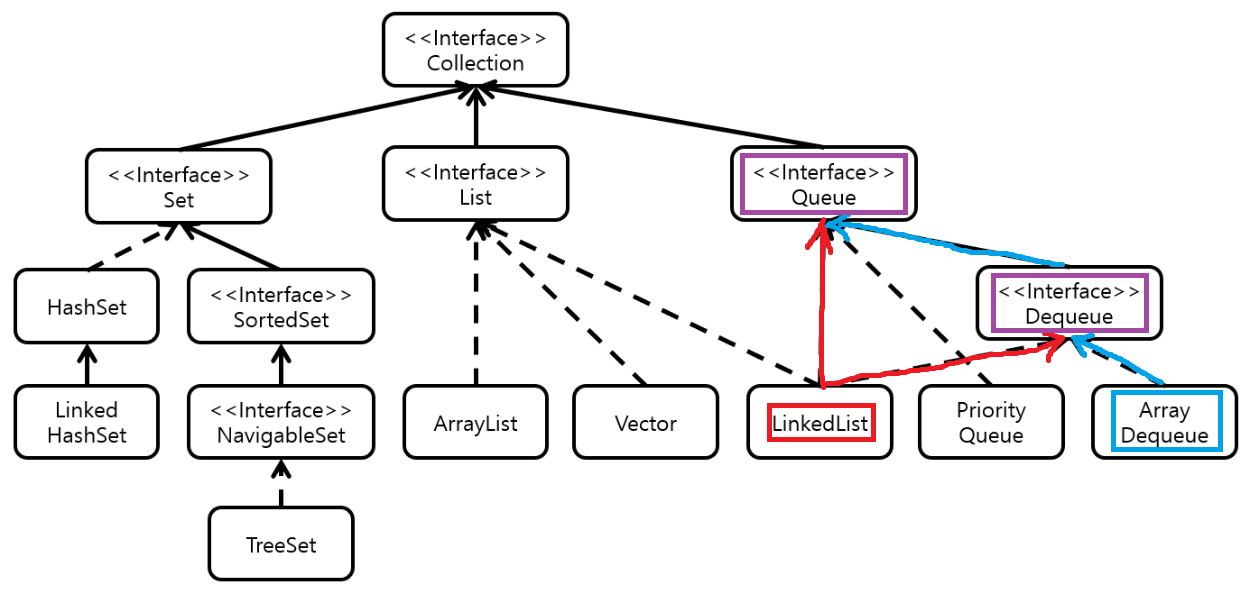
1. 큐는 인터페이스이고, 이를 구현하는 구현 클래스를 참조하게 업캐스팅하여 사용해야 한다.
e.g. Queue<> queue = new LinkedList<>(); || Queue<> queue = ArrayDequeue<>();
좌변과 우변의 타입이 일대일 대응(?)되는 형태의 컬렉션들은 모두 그 자체로 구현 클래스여서 그러하다.
하지만 큐는 그렇지 않으므로 LinkedList나 ArrayDequeu같은 구현 클래스를 통해서 사용할 수 있다.
2. 인덱스를 써야하는 상황에선 LinkedList를, 다른 경우은 ArrayDequeue가 더 성능이 좋다.
아래 자바 컬렉션 상속도를 보면 알겠지만, LinkedList는 Queue인터페이스와 Dequque 인터페이스를 모두 구현한다.
그리고 ArrayDequeue는 Dequeue 인터페이스를 구현하는데 Dequeue 인터페이스는 Queue 인터페이스를 상속하므로
결론적으로 큐든 데크든 둘 다 LinkedList와 ArrayDequeue 모두 사용할 수 있다.
(헷갈리면 뭐든 생각 나는 것을 써도 괜찮다는 뜻)
3. 큐에서의 추가 메소드는 offer이고, 삭제 메소드는 poll이다.
삭제 메소드 poll은 삭제된 값을 반환한다.
큐를 배열로 구현..?🤔
큐를 선형 배열로 구현하는 것에는 한계가 있다.
배열에서 삭제된 영역은 빈 공간으로 남게 되고,
추가하는 공간은 한정적이므로 배열이 가진 전체 길이를 비효율적으로 사용한다는 문제가 발생한다.
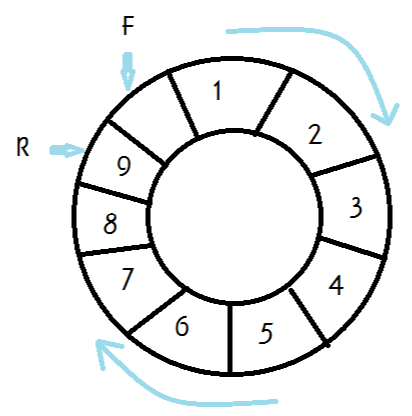
환형 큐를 배열로 구현
이 문제는 front나 rear이 배열의 길이를 넘어가면, mod연산을 해줌으로써 해결 가능하다.
또 원소가 삭제되면 front를 +1 / 원소가 추가되면 rear을 +1 해주면 된다.
시작은 아무것도 추가되지 않은 상태이므로 front=rear=0으로 초기화해준다.
여기서 또 다른 이슈가 발생하는데, 아무것도 추가 되지 않은 상태에서 front=rear=0이라면,
처음부터 하나의 빈 원소를 가지고 시작하는 것이 된다.
따라서 환형 큐를 구현할 때는 위의 두가지 특징
1.mod 연산을 통해 환형을 구현 / 2.하나의 빈 원소를 가짐 을 고려하면서 환형 큐를 구현해야 한다.
코드
class Queue {
int[] arr;
int front = 0;
int rear = 0;
Queue(int size) {
// 처음 시작할 때 하나의 빈 원소를 가지고 시작하므로 +1 해줘야 의도한 공간을 쓸 수 있음
this.arr = new int[size+1];
}
public boolean isEmpty() {
if (front == rear) {
return true;
} else {
return false;
}
}
public boolean isFull() {
if ((rear+1)%(arr.length) == front) {
return true;
} else {
return false;
}
}
public void enqueue(int data) {
if(isFull()){
System.out.println("Queue is full!");
} else {
rear = (rear+1)%arr.length;
arr[rear] = data;
}
}
public Integer dequeue() {
if(isEmpty()){
System.out.println("Queue is empty!");
return null;
} else {
// 보통은 업데이터 하기 전에 값을 저장하고, 업데이트 하고, 저장한 값을 리턴하겠지만,
// front가 가리키는 것은 항상 비어있는 것이므로 업데이트를 한 값을 바로 리턴하는 것임
front = (front+1)%arr.length;
return arr[front];
}
}
public void print() {
int start = (front+1)%arr.length;
int end = (rear+1)%arr.length;
// for문의 두번째 조건식에서 i<end를 쓰면, 환형 구조를 고려하지 않는 것
// 따라서 rear보다 한칸 더 뒤에 있는 것에 도달하기까지 for문을 굴리되, *부등호가 아니라 등호를 사용해야 함*
for (int i = start; i !=end ; i = (i+1)%arr.length) {
System.out.print(arr[i]+" ");
}
System.out.println();
}
}'Algorithm > 자료구조 구현' 카테고리의 다른 글
| [자료구조] Stack 구현 (0) | 2023.07.14 |
|---|---|
| [자료구조] Circular Doubly LinkedList 구현 (0) | 2023.07.14 |
| [자료구조] Doubly LinkedList 구현 (0) | 2023.07.14 |
| [자료구조] Singly LinkedList 구현 (0) | 2023.07.14 |
| [자료구조] LinkedList 란? (0) | 2023.07.14 |

