※ 본 글은 한경훈 교수님의 머신러닝 강의를 정리, 보충한 글입니다. ※
퍼셉트론이란?
퍼셉트론은 신경 세포 뉴런을 수학적으로 모델링한 초기 인공신경망(Artificial Neural Network)이다.
퍼셉트론은 다수의 입력으로부터 하나의 결과를 도출한다.
퍼셉트론은 뉴런을 모델링한 것이므로, 뉴런의 작동법과 비슷한 방식이 적용된다.
뉴런의 작동법
가지 돌기(Dendrite) : 주변 뉴런으로부터 전기신호를 받아들인다.
시냅스(Synapse) : 뉴런의 축삭 말단과 가지 돌기 사이의 공간으로, 전기신호의 세기를 재조정한다.
세포체(Soma, cell body): 가지돌기에서 받은 전기신호들이 합쳐진다.
축삭돌기(Axon) : 세포체의 전위가 일정 이상이면 이웃 뉴런으로 전기신호를 보낸다.
위의 뉴런작동법이 퍼셉트론에도 그대로 적용된다.
퍼셉트론의 작동법
- 뉴런과 마찬가지로 여러 입력으로부터 하나의 결과(1 or 0)를 출력한다.
ex. 전기가 흐른다 = 1 = True , 전기가 흐르지 않는다 = 0 = False - 시냅스에서 신호세기가 재조정되는 것처럼, 고유의 가중치가 입력 신호에 곱해진다.
이때 가중치가 클수록 해당 신호가 중요함을 의미한다. - 가중치(w) * 입력신호(x)의 모든 합이 임계값(theta)을 넘을때만 1을 출력한다.

net 함수 : 모든 입력값과 그에 대응하는 가중치 곱의 총합을 구하는 함수
활성화 함수 : net 값과 임계값 theta를 비교하여 0 또는 1을 출력하는 함수
논리회로를 퍼셉트론으로 구현하기
두 개의 입력이 있는 퍼셉트론을 구현한다면, 각 입력에 대응하는 가중치 w_1, w_2와 편향 b (bias)를 설정해야 한다.
cf. 이때 편향이란, 임계치의 마이너스를 의미한다. -> b = - θ
x1w1 + x2w2 ≤ θ 를 조사하는 것 보다
x1w1 + x2w2 + b ≤ 0를 조사하는 것이 더 직관적이므로 편향 b가 임계치 theta 보다 더 자주 쓰인다.
논리회로를 구현하기 위해선 파이썬 numpy의 array, sum 메서드를 사용해야 한다.
array 메서드는 리스트 데이터 타입을 벡터로 바꿔준다.
백터는 연산이 쉽다는 장점이 있다.
ex. 벡터 1 * 벡터 2 ⇒ 좌표끼리의 곱인 벡터 3
sum 메서드는 벡터의 모든 원소의 합을 리턴한다.
가중치와 임계값을 설정할 때, 해당 게이트의 기하학적 의미를 생각하면 쉬워진다.
AND 게이트
모두 참이어야만 참 출력
(w1, w2, theta) = (0.5, 0.5, 0.7)
# AND
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
inputs = [(0, 0), (1, 0), (0, 1), (1, 1)]
print('AND :')
for x1, x2 in inputs:
y = AND(x1, x2)
print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))
# AND :
# (0, 0) -> 0
# (1, 0) -> 0
# (0, 1) -> 0
# (1, 1) -> 1
NAND 게이트 (not and)
AND 게이트에 not을 붙인 것이므로 가중치, 편향을 음수로 바꾸면 됨.
(w1, w2, theta) = (-0.5, -0.5, -0.7)
# NAND
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
inputs = [(0, 0), (1, 0), (0, 1), (1, 1)]
print('NAND :')
for x1, x2 in inputs:
y = NAND(x1, x2)
print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))
# NAND :
# (0, 0) -> 1
# (1, 0) -> 1
# (0, 1) -> 1
# (1, 1) -> 0
OR 게이트
둘 중 하나만 참이더라도 참 출력
(w1, w2, theta) = (0.5, 0.5, 0.2)
# OR
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
inputs = [(0, 0), (1, 0), (0, 1), (1, 1)]
print('OR :')
for x1, x2 in inputs:
y = OR(x1, x2)
print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))
# OR :
# (0, 0) -> 0
# (1, 0) -> 1
# (0, 1) -> 1
# (1, 1) -> 1
XOR 게이트
논리 값이 다를 때만 참 출력
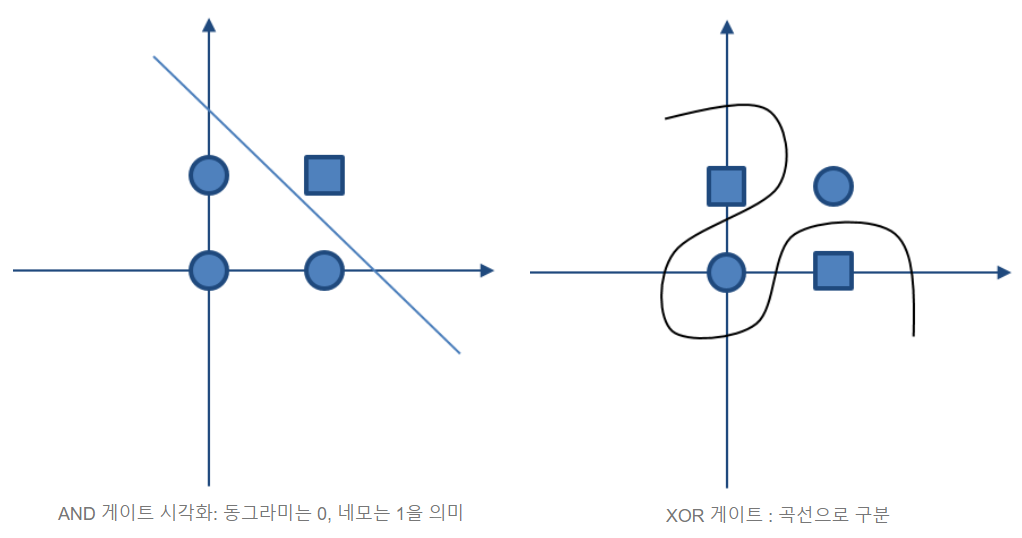
⇒ 단층 퍼셉트론으론 구현할 수 없음
ex. (0,0) -> 0 , (1,0) ->1, (0,1) ->1, (1,1) -> 0
XOR 게이트를 단층 퍼셉트론으로 구현할 수 없는 이유
단층 퍼셉트론으로 구현된 논리 게이트를 기하학적으로 해석하면,
좌표평면 위에 (0,0) (0,1) (1,0) (1,1) 의 점들이 있을 때 직선으로 참과 거짓을 분리하는 작업이다.
XOR 게이트는 직선으로 점들을 분리할 수 없으므로, 다중 퍼셉트론으로 구현되어야 한다.
단층 퍼셉트론은 직선형 영역만 표현할 수 있지만, 다중 퍼셉트론은 비선형 영역도 표현할 수 있다.
다중퍼셉트론으로 XOR 구현
AND, NAND, OR의 다중 구조로 XOR 게이트를 구현할 수 있다.
OR과 NAND의 AND 가 XOR 이므로, 아래와 같이 표현할 수 있다.

def XOR(x1, x2):
return AND(NAND(x1,x2), OR(x1,x2))
inputs = [(0, 0), (1, 0), (0, 1), (1, 1)]
print('XOR :')
for x1, x2 in inputs:
y = XOR(x1, x2)
print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))
# XOR :
# (0, 0) -> 0
# (1, 0) -> 1
# (0, 1) -> 1
# (1, 1) -> 0
'ML' 카테고리의 다른 글
| [ML] 딥러닝 1 - 6강 손실함수 (0) | 2021.07.23 |
|---|---|
| [ML] 딥러닝 1 - 5강 신경망 구현 (0) | 2021.07.23 |
| [ML] 딥러닝 1 - 4강 MNIST (0) | 2021.07.17 |
| [ML] 딥러닝 1 - 3강 인공신경망 (0) | 2021.07.14 |
| [ML] 딥러닝 1 - 2강 활성화 함수 (1) | 2021.07.13 |



