※ 본 글은 한경훈 교수님의 머신러닝 강의를 정리, 보충한 글입니다. ※
이전 글 복습
앞서 배운 손실 함수는 '실제 값과 예측 값의 차이를 수치화'하는 함수였다.
손실 함수의 종류로는 1. 평균 제곱 오차 2. 교차 엔트로피가 있었다.
두 손실 함수 모두 두 확률분포(실제 vs 예측) 사이의 거리를 나타내는 함수이다.
이때 평균 제곱 오차의 경우 거리를 나타낸다는 사실을 직관적으로 받아들일 수 있는 반면
교차 엔트로피의 경우 한 번에 의미를 받아들이기 힘들다.
교차 엔트로피는 손실 함수로 자주 사용되는 함수이므로, 정보이론을 바탕으로 이를 설명하고자 한다 (증명 x).
엔트로피
정보이론에서 엔트로피는 불확실성을 수치화한 값이다.
다른 말로 이해하면 최적의 전략 하에서 그 사건을 예측하는 데에 필요한 질문 개수를 의미한다.
따라서 엔트로피가 감소하는 것은 사건을 맞추기 위한 질문이 줄어든다는 뜻이므로 정보량이 줄어든다는 의미가 된다.
이렇게 엔트로피를 사용하면 정보를 수학적으로 나타낼 수 있다. (-> 정보이론에서 엔트로피의 의의)
예를 들어, a, b, c, d 4장의 카드 중 한 장을 뽑는 사건을 가정해보자.
가장 먼저 'a인가?'라는 질문을 할 수 있다.
질문은 하나이며, 이 질문에 대해 답을 얻을 확률은 1/2이다.
두 번째로 'b인가?'라는 질문을 할 수 있다.
앞선 질문과 이번 질문을 합하면 총 2개의 질문이며, 답을 얻을 확률은 1/4이다.
세 번째로 'c인가?'라는 질문을 할 수 있다.
총 3개의 질문이며, 답을 얻을 확률은 1/8이다.
다음으로 'd인가?'라는 질문을 할 수 있지만, 이경우 질문에 대한 답을 볼 필요도 없이 남은 카드는 무조건 d이므로 세 번째 질문과 동일한 확률이다.
위 예시를 통해 예측에 필요한 질문 개수의 평균을 계산하면 아래와 같다.
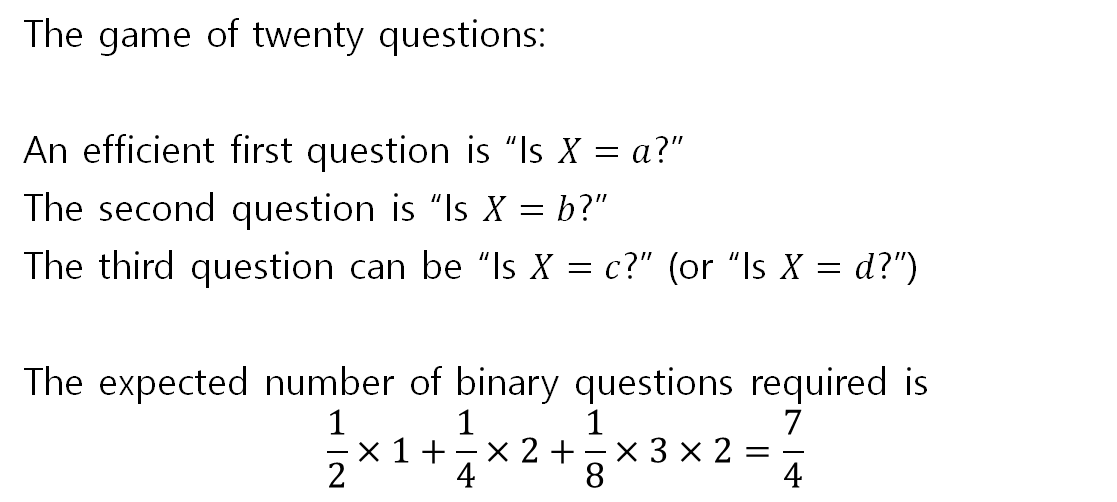
위 수식을 일반화하면 아래와 같다.
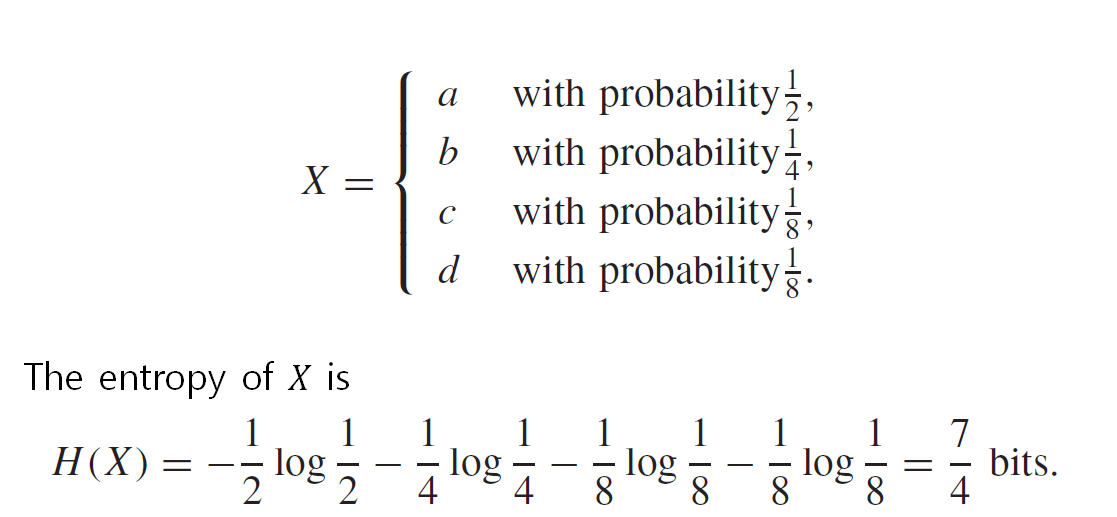
엔트로피의 수식
위 방법으로 엔트로피를 정리하면, 사건 X에 대한 확률분포를 p(x)라고 할 때 엔트로피 H(x)는 아래와 같이 표현할 수 있다.
모든 확률분포에 x log x를 취하고 다 더한 후 - 를 붙이면 된다.

엔트로피의 성질
앞서 엔트로피는 불확실성을 수치화한 값이라고 했다.
불확실성이 가장 커질 때는 확률변수가 모두 1/n일 때(모든 경우의 확률이 같을 때)이고 이때 엔트로피는 최대 값인 logn을 갖는다.
예를 들어, 동전을 던지는 사건에서의 확률분포는 (1/2, 1/2) 이므로 엔트로피는 - (1/2 * log1/2 + 1/2 * log1/2) = 1이다. 따라서 엔트로피는 아래 공식을 만족한다.
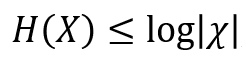
교차 엔트로피
교차 엔트로피를 유도하기 위해선 상대 엔트로피(쿨백-라이블러 발산 또는 KLD)를 배울 필요가 있다.
상대 엔트로피는 두 확률분포의 차이를 계산하는 함수이다.
상대 엔트로피의 공식 아래와 같다.

하지만 상대 엔트로피는 비대칭으로, p와 q의 위치를 바꾸면 값이 달라지는데,
이는 수학에서 '거리'의 정의를 위반하는 것이므로 상대 엔트로피만으론 두 확률분포 사이의 거리를 나타낼 수 없다.
cf. 선분 AB와 선분 BA의 길이가 다르다면, 이를 A와 B사이의 거리로 정의할 수 없는 것과 같은 원리이다.
따라서 두 확률분포 사이의 거리를 나태 내기 위해선, 상대 엔트로피에서 '상대적'이라는 개념을 제외할 필요가 있다.
원래의 상대 엔트로피 H(p, q) - H(p)에서 p의 엔트로피인 H(p)를 좌변으로 넘겨서 상대적이라는 개념을 없애면
우변에 H(p, q)만이 남는다.
이렇게 H(p, q)로 두 확률분포 p와 q 사이의 거리를 나타낼 수 있으며, 이를 교차 엔트로피라고 한다.
두 확률분포 사이의 거리는 곧 두 확률분포가 얼마나 닮았는지를 나타낸다.
따라서 교차 엔트로피 값은 예측의 틀린 정도를 나타내는 손실 함수의 역할을 할 수 있는 것이다.
q가 p에 가까울수록 즉, 예측값이 실제값과 가까울수록 교차 엔트로피의 값은 줄어든다.
'ML' 카테고리의 다른 글
| [ML] 딥러닝 1 - 9강 경사하강법 (0) | 2021.08.03 |
|---|---|
| [ML] 딥러닝 1 - 8강 수치미분과 gradient (0) | 2021.07.29 |
| [ML] 딥러닝 1 - 6강 손실함수 (0) | 2021.07.23 |
| [ML] 딥러닝 1 - 5강 신경망 구현 (0) | 2021.07.23 |
| [ML] 딥러닝 1 - 4강 MNIST (0) | 2021.07.17 |



