Intro.
- 수치미분 vs 미분공식 + 연쇄법칙
역전파는 미분공식과 연쇄법칙을 이용하여 미분 계산을 간단히 한 방식이다.
후자의 경우가 더 계산이 간단하다는 것은 간단히 생각해봐도 알 수 있는 사실이다.
이전 글에서 비유한 것 처럼, 수치미분은 미분의 정의를 그대로 적용한 것이고 - 역전파가 '역'전파인 이유..? 🤔 by 교수님 피셜
이를 위해선 밖에 있는 함수 먼저 미분하고 이후에 안의 함수를 미분해야 하는데,
ex. h(g(f(x))) → h'(g(f(x)))g'(f(x))f'(x)
이 방향이 역방향 같다고 생각되어 '역' 전파라 불리게 되었다.
역전파에서 연쇄법칙을 적용할 때, 흔히 '겉미분 후 속미분(합성함수 미분)'이라 불리는 공식을 적용해야 한다.
계산 그래프
역전파의 원리를 계산 그래프로 이해해보자.
많은 딥러닝 프레임워크들이 계산 그래프를 기반으로 하고 있으므로 익숙해질 필요가 있다.
ex. 대표적 프레임 워크인 텐서플로우는 모든 프로그램이 계산 그래프를 통해 구현되어있음
순전파의 계산 그래프
순전파의 계산 그래프는 별도 설명 없이도 직관적으로 이해할 수 있다.

역전파의 계산 그래프
1로 출발하여 오른쪽에서 왼쪽으로 흘러간다.
- 곱셈 노드의 역전파 규칙
반대편 값을 엇갈려 곱하여 흘려보낸다. - 덧셈 노드의 역전파 규칙
그냥 흘려보낸다.

역전파 계산 그래프 결과의 갖는 의미
이유를 모르고 '곱셈은 엇갈려 곱하고 덧셈은 그냥 흘러보낸다'라는 규칙으로 계산을 했지만,
놀랍게도 결과값은 함수를 해당 변수로 편미분했을 때, 나머지 변수를 대입한 값이었다.
ex. 사과 하나의 가격 : x, 사과 개수 : y, 소비세 : z 일 때, 소비세 : xyz 이다.
x로 xyz를 편미분하면 yz가 되는데 y = 2, z = 1.1 을 대입하면 역전파의 결과 값인 2.2가 나온다.
역전파 계산이 편미분 결과가 되는 이유
역전파는 이전 식의 국소적 미분을 곱하는 방법으로 진행된다.
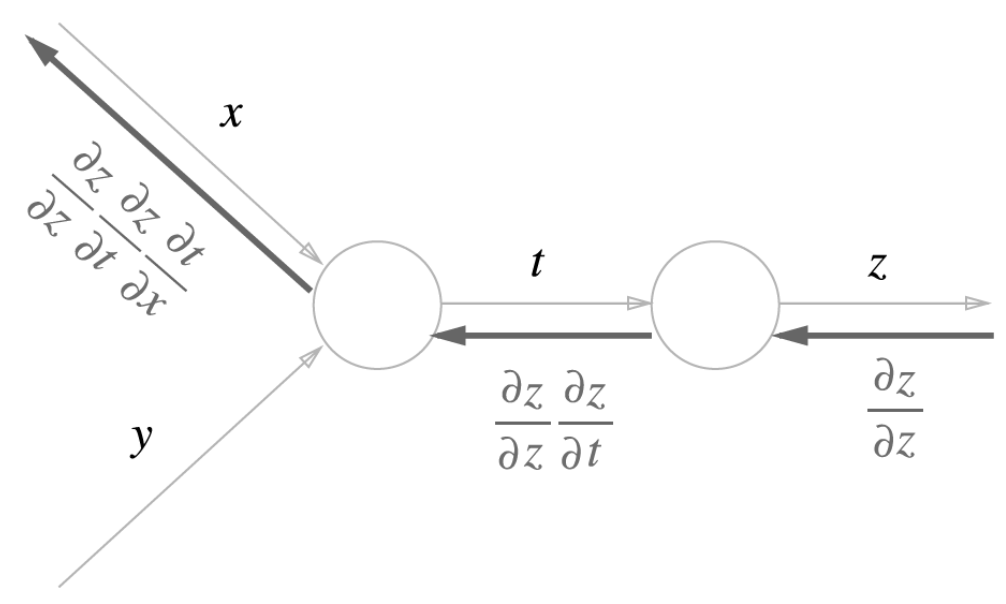
예를들어, 자기 자신에 대한 국소적 미분은 dz/dz 이므로 1로 시작하고
z에서 t로 가기 위해선 z에 대한 t의 국소적 미분인 dz/dt을 곱해준다.
또 t에서 x로 가기 위해선 t에 대한 x의 국소적 미분인 dt/dx을 곱해준다.
이러한 과정을 거치면 x의 역전파 값은 dz/dz * dz/dt * dt/dx 즉, dz/dx 가 되는데 이는 z에 대한 x의 편미분 값이다.
따라서 역전파의 계산 결과값이 편미분의 결과 값이 되고, 역전파의 과정은 연쇄법칙의 과정이 된다.
덧셈 역전파를 그대로 흘려보내고, 곱셈 역전파는 엇갈려 곱한다는 규칙은
덧셈 역전파는 이전 식에 대해 국소적 미분의 값이 1이므로 1을 곱하는 것이고,
곱셈 역전파는 이전 식에 대해 국소적 미분의 값이 엇갈린 식이기 때문에 그렇다.
ex. x + y = f 일때, df/dx = 1 이고 xy =f 일때, df/dx = y 이다.
덧셈 역전파 구현
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy
곱셈 역전파 구현
class MulLayer:
def __init__(self):
self.x = None
self.y = None
# 순전파
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
# 역전파
def backward(self, dout):
dx = dout * self.y # x와 y를 바꿔 곱한다.
dy = dout * self.x
return dx, dy
역전파 계산 구현

apple = 100
apple_num = 2
tax = 1.1
# 계층들
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()
# 순전파
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)
print('%d' % price)
# 역전파
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)
print("price:", int(price)) # 220
print("dApple:", dapple) # 2.2
print("dApple_num:", int(dapple_num)) # 110
print("dTax:", dtax) # 200
이미지 출처 : https://deep-learning-study.tistory.com/16
참고 and 코드 출처 : https://excelsior-cjh.tistory.com/171
'ML' 카테고리의 다른 글
| [ML] 훈련 세트와 테스트 세트 (0) | 2021.10.28 |
|---|---|
| [ML] K-최근접 이웃 알고리즘(KNN) (0) | 2021.10.28 |
| [ML] 딥러닝 1 - 10강 수치미분을 통한 학습 구현 (0) | 2021.08.22 |
| [ML] 딥러닝 1 - 9강 경사하강법 (0) | 2021.08.03 |
| [ML] 딥러닝 1 - 8강 수치미분과 gradient (0) | 2021.07.29 |

