※ 본 글은 한경훈 교수님의 머신러닝 강의를 정리, 보충한 글입니다. ※
[딥러닝I] 10강. 수치미분을 통한 학습 구현 - YouTube
지금까지 배운 지식들을 동원해 MNIST 데이터 분류 모델을 학습시켜보자.
구현해야 하는 모델은
1. 2층 신경망이며, 각 층마다 뉴런의 개수는 784, 50, 10개이다.
2. 손실 함수는 교차 엔트로피이고 손실함수의 변수(편향와 가중치) 개수는
총 784 × 50 + 50 + 50 × 10 + 10 = 39,760 개다.
3. learning rate = 0.1 , 학습 회수 = 10,000로 설정한다.
4. 학습 회수만큼 반복하여 −𝑙⋅𝛻𝑓을 더하여 weight와 bias를 업데이트한다.
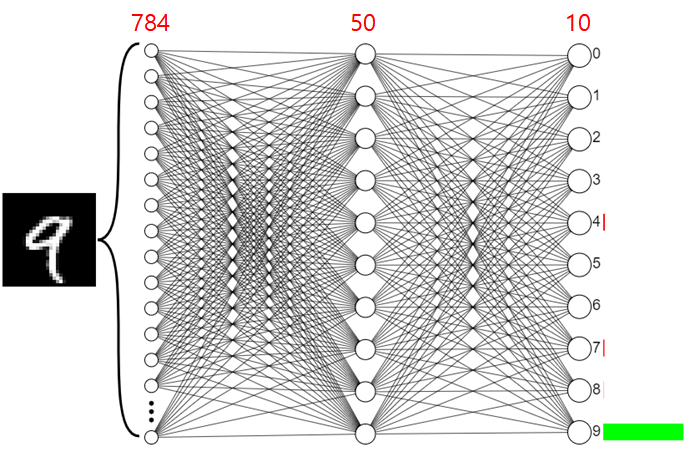
MNIST 분류 모델 구현
# coding: utf-8
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
# input_size는 입력되는 데이터의 크기가 아닌 입력층의 뉴런 개수이다.
# hidden_size는 은닉층의 뉴런 개수이다.
# output_size는 출력되는 데이터의 크기가 아니라 출력층의 뉴런 개수이다.
# weight_init_std는 가중치의 초기 표준편차이다.
# 평균이 0이고 표준편차가 1인 표준 정규분포에서 랜덤하게 가중치를 정하는 것이 아닌,
# 평균이 0이고 표준편차가 0.01인 정규분포에서 가중치를 정하도록 설정하는 것이다.
# 우리가 만들 모델의 형태를 생각하면 TwoLayerNet(784,50,10)으로 매개변수를 지정해야 한다.
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 가중치 초기화 - 뉴럴 네트워크의 모든 변수(편향, 가중치)를 딕셔너리에 담아서 관리한다.
self.params = {}
# 일반적으로 초기(init) 가중치는 정규분포를 따라 랜덤하게 선택하고 편향은 제로 벡터로 둔다.
# 입력층과 은닉층을 연결하는 가중치 이므로 (input_size, hidden_size) 크기의 행렬을 사용한다.
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
# 은닉층에 사용되는 편향이므로 (hidden_size) 크기의 0으로 가득 찬 행렬을 사용한다.
36['b2'] = np.zeros(output_size)
# 예측
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
# Affine -> Sigmoid -> Affine -> Softmax
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# 손실함수
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
# 정확도 측정
def accuracy(self, x, t):
y = self.predict(x)
# axis = 1일때 즉, 행에서 가장 값이 큰 인덱스를 리턴한다.
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# 수치미분을 하고 변수로 편향이랑 가중치를 넣는 과정이 한번에 이해가지 않네.. ㅠ
# 그리고 loss_W는 정말이지.. 무슨 역할인지 잘 모르겠다..!
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
# 아래 내용은 역전파에 해당하는 내용으로 이번엔 일단 pass!
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
MNIST 분류 진행하기
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
# 데이터 읽기
# normalize를 True로 하는 의미 : 픽셀 값을 255로 나눠 0~1 사이 값으로 나타내겠다는 뜻
# one_hot_label을 True로 하는 의미 : 0-9 정수를 원핫벡터로 변환
# flatten은 디폴트가 True 이므로 여기선 생략
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 하이퍼파라미터
iters_num = 10000 # 반복 횟수를 10000번으로 설정
train_size = x_train.shape[0] # x_train.shape() = (60000, 784) 이므로 train_size는 60000 이다.
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 1 에폭 당 반복 수 (epoch이란, 훈련 데이터를 다 소진하는 하나의 구간을 의미함)
# ex. MNIST에서는 1에폭당 6만장의 훈련 데이터가 사용된다.
# 아래 코드의 의미는 한 에폭당 배치 사이즈만큼 즉 (train_size / batch_size = 600번) 반복된다는 뜻이다.
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
# 미니배치 획득
# train_size 이하의 정수 중 batch_size 만큼을 랜덤 추출하라는 뜻
batch_mask = np.random.choice(train_size, batch_size)
# 인덱스가 랜덤 추출한 정수에 해당하는 데이터를 추출
# -> 학습 데이터를 batch_size 만큼 랜덤하게 추출할 수 있음
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
# 손실함수의 수치 gradient함수에 가중치와 편향을 넣은 결과를 딕셔너리로 리턴받음
# grad = network.gradient(x_batch, t_batch) -> 역전파 이용
grad = network.numerical_gradient(x_batch, t_batch)
# 매개변수 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 1 에폭 당 정확도 계산
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
수치 미분의 한계와 역전파
위 코드에서 수치 미분으로 모델을 학습시키기 위해선 39,760×10,000번의 수치미분 계산이 필요하다.
또한 수치 미분이 적용되는 함수는 affine + sigmoid + softmax + 교차 엔트로피를 합성한 복잡한 함수이므로
학습하는데에 너무 많은 메모리와 시간이 사용된다.
때문에 수치 미분 이외에 미분을 더 간단하게 할 ⭐새로운 방식⭐이 필요하다.
고등 수학에서 미분을 처음 배웠을 때는 평균 변화율의 극한으로 배웠지만,
복잡한 미분을 해야 할 때는 미분 공식을 적용하여 빨리 풀었던 경험이 있을 것이다.
이와 비슷하게 각 층에서의 미분을 공식화하여 미분 과정을 단순화하는 방법이 바로 '역전파' 방법이다.
역전파는 사람이 Affine층, Sigmoid층, SoftMax층, 손실 함수층에서 각각 미분 공식을 이용하여 직접 미분한 후
chain rule(연쇄 법칙 or 합성함수의 미분)을 써서 전체 미분을 구해 코딩하는 알고리즘이다.
각 층에 미분 공식을 적용해보면 덧셈과 곱셈으로 표현되는데,
컴퓨터가 가장 빨리 할 수 있는 계산이 덧셈과 곱셈이므로 수치 미분보다 빠른 계산이 가능해진다.
'ML' 카테고리의 다른 글
| [ML] K-최근접 이웃 알고리즘(KNN) (0) | 2021.10.28 |
|---|---|
| [ML] 딥러닝 1 - 11강 계산 그래프 (0) | 2021.08.29 |
| [ML] 딥러닝 1 - 9강 경사하강법 (0) | 2021.08.03 |
| [ML] 딥러닝 1 - 8강 수치미분과 gradient (0) | 2021.07.29 |
| [ML] 딥러닝 1 - 7강 엔트로피 (0) | 2021.07.29 |


