합성곱과 풀링
합성곱 신경망(CNN)은 합성곱 계층 (convolutional layer)과
풀링 계층 (pooling layer)이라고 하는 새로운 층을 fully-connected 계층 이전에 추가함으로써
원본 이미지에 필터링 기법을 적용한 뒤에 -> 합성곱 계층, 풀링 계층
필터링된 이미지에 대해 분류 연산이 수행되도록 구성된다. -> fully-connected 계층
합성곱 계층은 이미지에 필터링 기법을 적용해 특징을 추출하고,
풀링 계층은 이미지의 국소적인 부분들을 하나의 대표적인 스칼라 값으로 변환함으로써
이미지의 크기를 줄이는 등의 다양한 기능들을 수행한다.

합성곱 신경망의 필요성
이미지를 DNN으로 처리하기 위해선 벡터화(flatten) 시켜 DNN에 입력해야 하는데,
이때 이미지가 가진 공간적인 구조에 대한 정보가 유실된다.

결국 이미지의 공간적인 구조 정보를 보존하면서 학습할 수 있는 방법이 필요해졌고, 이를 위해 사용하는 것이 합성곱 신경망이다.
채널
이미지는 (높이 x 너비 x채널)이라는 3차원 텐서이다.
여기서 높이는 세로의 픽셀 수, 너비는 가로의 픽셀 수, 채널(or깊이)는 색 성분 을 의미한다.
ex. 28x28 픽셀로 이뤄진 컬러 이미지 : (28,28,3)
합성곱 연산
합성곱이란, 행렬에서 같은 위치에 있는 것들을 곱한 후 그 값을 다 합하는 연산이다.
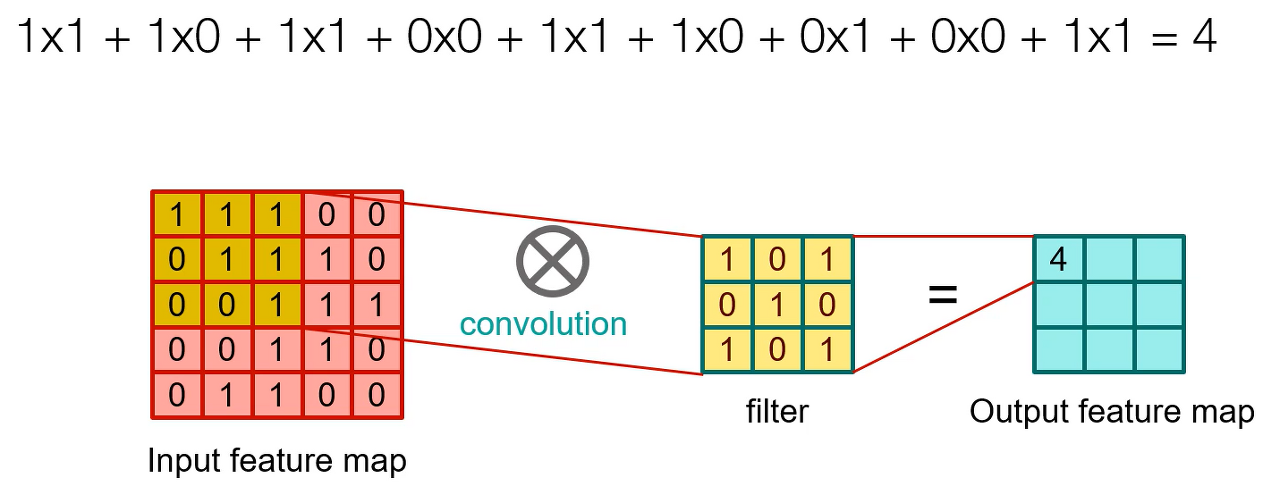
합성곱 층에서는 커널(kernel) 혹은 필터(filter)가 이미지를 처음부터 끝까지 겹치며 훑으면서 합성곱 연산을 수행한다.
커널의 이동량을 스트라이드(stride)라고 하며 stride의 값은 바꿀 수 있다.
합성곱 연산으로 얻어지는 행렬을 특성맵(feature map)이라 한다.
합성곱 연산의 결과인 feature map의 크기는 입력 이미지의 크기보다 작아진다.
따라서 합성곱 층을 여러 번 쌓으면 가장자리에 위치한 픽셀들의 정보는 점점 사라지고, feature map은 초기 입력보다 매우 작아진다는 문제가 발생할 수 있다.
이러한 문제점을 해결하기 위해 이용되는 것이 패딩 (padding)이다.
패딩
입력 이미지의 가장자리에 특정 값으로 설정된 픽셀들을 추가함으로써
입력 이미지와 출력 이미지의 크기를 같거나 비슷하게 만드는 역할을 수행한다.
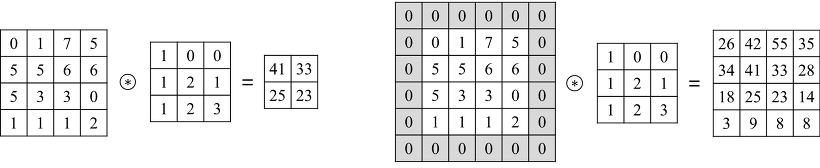
대표적인 패딩으로는 가장자리에 0을 추가하는 zero padding이 있다.
위 예시의 왼쪽에서는 4x4 이미지에 3x3 커널을 합성곱 하여 2x2 feature map을 얻었지만
오른쪽에서는 4x4 이미지에 zero padding을 해서 6x6으로 만들고 3x3 커널을 합성곱하여 4x4 feature map을 얻었다.
-> 입력 이미지와 출력 이미지의 크기가 같아짐
합성곱 층
추가로 합성곱 연산이 끝난 후 비선형성을 추가하기 위해 ReLU 함수를 통과시켜야 한다.
이렇게 합성곱 연산, ReLU, 패딩 처리를 해주는 부분을 합성곱 층이라 한다.
이처럼 합성곱층은 이미지 데이터의 특징을 추출하고 압축하는 역할을 한다.
따라서 합성곱층을 특징추출기(Feature Extractor)라고 부르기도 한다.
합성곱 신경망의 가중치 (feat. CNN은 어떻게 공간 정보를 유지하나?)
앞에서 배운 합성곱 연산을 인공 신경망의 관점으로 표현하면 아래와 같다.

이때 가중치 w는 커널의 원소이고, 입력 x는 커널과 겹쳐지는 픽셀임을 알 수 있다.
이미지의 모든 픽셀을 사용하는 것이 아니라 각 합성곱 연산마다 '필터와 겹쳐지는 부분'의 픽셀만 사용하므로
결국 합성곱 신경망은 다층 퍼셉트론을 사용할 때보다 훨씬 적은 수의 가중치를 사용하며 공간적 구조 정보를 보존할 수 있는 것이다.
합성곱 신경망의 편항
합성곱 신경망에서도 편향을 추가할 수 있다.
편향은 커널을 적용한 뒤에 더해진다.
편향은 하나의 값(스칼라)만 존재하며, 브로드캐스트를 통해 커널이 적용된 결과의 모든 원소에 더해진다.
다수의 채널을 가질 경우 합성곱 연산
입력 이미지의 채널과 커널의 필터 수는 동일해야 한다.
따라서 입력 이미지가 3개의 채널을 가질 경우, 커널의 채널도 3개여야 한다.
각 채널에 해당하는 이미지, 커널끼리 합성곱 연산을 수행한 후 결과를 모두 더하여 하나의 faeture map을 구한다.

여러 커널을 사용할 경우 각 커널에 대해 feature map이 하나씩 나오므로 feature map의 채널 수는 커널의 수와 같다.
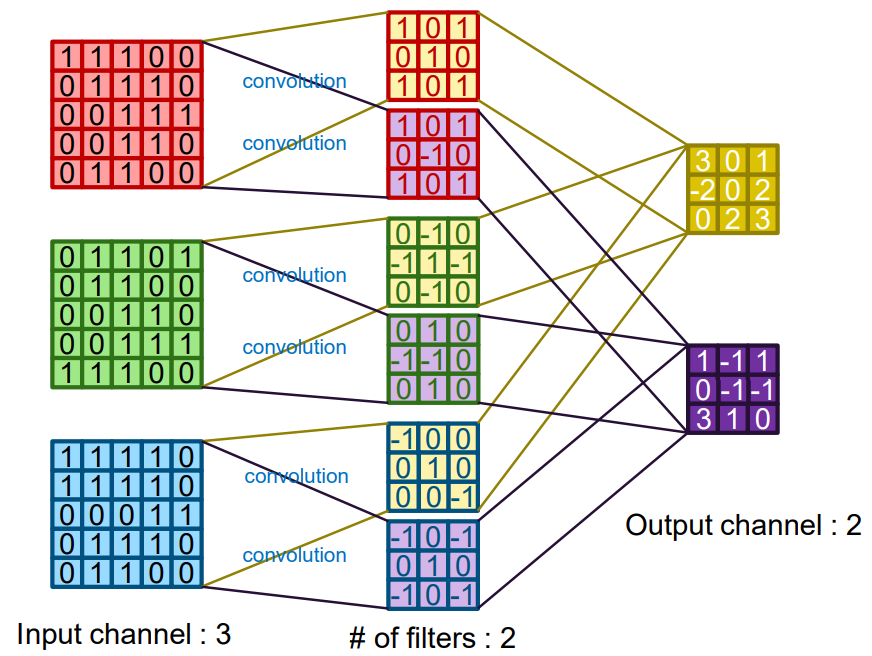
⭐정리
- 입력 이미지의 채널 수와 커널의 수는 동일
- 커널 수와 피쳐맵의 채널 수는 동일
풀링 (Pooling)
이미지 데이터의 특징은 인접 픽셀들 간의 유사도가 매우 높다는 것이다.
따라서 이미지는 픽셀 수준이 아니라, 특정 속성을 갖는 국소 영역 수준으로 표현될 수 있으며,
풀링 계층은 이미지 데이터의 이러한 특징을 바탕으로 설계되었다.
풀링 계층은 이미지의 국소적인 부분들을 하나의 대표적인 스칼라 값으로 변환함으로써
이미지의 크기를 줄이는 연산을 한다.
풀링 연산도 합성곱 연산과 마찬가지로 커널과 스트라이드의 개념을 가진다.
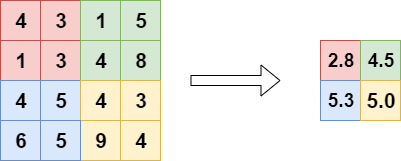
커널에 해당하는 픽셀들을 어떻게 하나의 스칼라로 나타내는지에 따라 풀링의 종류가 달라진다.
- Max Pooling : 커널에 해당하는 픽셀 중 최댓값을 취함 (더 많이 사용됨)

- Average Pooling : 커널에 해당하는 픽셀의 평균값을 취함
'ML' 카테고리의 다른 글
| [ML] Fashion MNIST (0) | 2022.02.13 |
|---|---|
| [ML] 타이타닉 생존자 예측하기 (0) | 2022.01.30 |
| [ML] 소프트맥스 회귀 (Softmax Regression) (1) | 2022.01.09 |
| [ML] 특성 공학과 규제 (1) | 2021.11.05 |
| [ML] 선형 회귀 (0) | 2021.11.04 |


