다중 분류(Multi Classification) 문제에서 많이 사용되는 소프트맥스 회귀에 대해 알아보자.
원-핫 인코딩 (One-hot encoding)
원-핫 인코딩이란, 범주형(category) 변수를 binary 하게 표현한 것이다.
선택해야 하는 선택지의 개수만큼의 차원을 가지며,
선택지의 인덱스에 해당하는 원소에는 1, 나머지 원소는 0의 값을 가지도록 하는 표현 방법이다.
원-핫 인코딩으로 표현된 벡터를 원-핫 벡터(one-hot vector)라고 한다.
ex. 0~9의 정수를 원-핫 인코딩으로 표현하면 0 = [1,0,0,0,0,0,0,0,0,0] , 5 = [0,0,0,0,0,1,0,0,0,0] 가 된다.
원-핫 인코딩의 특징 : 무작위성
원-핫 인코딩으로 나타낸 레이블은 모든 쌍에 대해서 유클리드 거리가 동일하다는 특징이 있다.
cf. 유클리드 거리 = 유클리드 공간에서의 거리, 고등학교 때 배운 '두 점 사이의 거리'를 생각하면 쉽다.
일반적으로 유클리드 거리는 클래스 간의 관계를 의미하는데,
원-핫 인코딩은 유클리드 거리가 동일하므로 클래스 간의 연관성이 없는 분류 문제에서 주로 사용한다.
예를 들어 ['강아지','고양이','개구리','도롱뇽'] 분류 문제에서는 강아지와 고양이, 개구리와 도롱뇽이 연관이 있다.
하지만, [주어진 손글씨가 0-9중 어떤 수인가?]를 분류하는 문제에서는 해당 수가 0인 것과 1인 것, 2인 것이 연관이 없으므로 원-핫 인코딩을 사용한다.
cf. 위 예시에서 정수 인코딩을 하면 예측값 = 2, y = 1일 때 MSE = 1 / 예측값 = 3, y = 1일 때 MSE = 4 이므로
'1과 2의 거리 < 1과 3의 거리' 즉, 1은 3보다 2와 가깝다는 정보를 줄 수 있다.
하지만 실제로 클래스간의 연관성은 없기 때문에 잘못된 정보를 기계에게 줄 수 있다.
-> 원-핫 인코딩으로 이런 문제 해결할 수 있음
소프트맥스 회귀 (Softmax Regression)
각 클래스마다 '정답일 확률'을 할당하며, 전체 클래스의 확률 합은 1이 되어야 한다.
소프트맥스 회귀에는 소프트맥스 함수가 사용된다.
소프트맥스 함수는 각 클래스에 대한 확률 벡터를 반환하는 함수이다.
ex. [주어진 손글씨가 0-2중 어떤 수인가?]의 결과가 [0.1, 0.1, 0.7] 이면 0일 확률 = 0.1, 1일 확률 = 0.1, 2일 확률 = 0.7을 의미한다.
이를 위해 (exp)를 적용하여 모든 원소를 양수로 바꿔주고, 산술평균을 적용하여 총합이 1이 되게 한다.
k차원 입력 벡터에 대해 $z_i$가 i번째 원소, $p_i$가 i번째 클래스일 확률이라 하면 $p_i$를 아래와 같이 정의한다.
$p_{i}=\frac{e^{z_{i}}}{\sum_{j=1}^{k} e^{z_{j}}}\ \ for\ i=1, 2, ... k$
ex. 클래스가 3개일 때 소프트맥스 함수가 반환하는 벡터
$softmax(z)=[\frac{e^{z_{1}}}{\sum_{j=1}^{3} e^{z_{j}}}\ \frac{e^{z_{2}}}{\sum_{j=1}^{3} e^{z_{j}}}\ \frac{e^{z_{3}}}{\sum_{j=1}^{3} e^{z_{j}}}] = [p_{1}, p_{2}, p_{3}] = \hat{y} = \text{예측값}$
교차 엔트로피
본 실습에서는 손실 함수로 교차 엔트로피 함수를 사용한다.
교차 엔트로피 함수는 두 확률 분포 사이의 거리를 구하는 함수이며,
본 실습에서는 'softmax로 구한 확률 벡터(예측값)'와 '정수를 원-핫 인코딩한 벡터(레이블)' 사이의 거리를 구하기 위해 사용된다.
즉, 예측값과 레이블 사이의 거리를 오차로 사용하는 함수이다.
엔트로피 함수 : 불확실성을 수치화한 값
$H(P) = -\sum_{i=1}^{n}p(x_{i})\ log_2p(x_{i})$
(n: 모든 사건의 수, $p(x_i)$: 사건이 일어날 확률)
교차 엔트로피 함수 : 두 확률 분포 사이의 거리
$H(P,Q) = -\sum_{i=1}^{k}q(x_{i})\ log_2p(x_{i})$
(k: 확률 분포의 차원, $p(x), q(x)$: 확률 분포)
손실 함수로서의 교차 엔트로피 : 교차 엔트로피의 평균
$cost(W) = - \frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{C} q(x_j)log_2(p(x_j))$
($n$: 데이터 수, $C$: 클래스 수, $q(x_j)$: 원-핫 벡터, $p(x_j)$: 소프트맥스의 확률 벡터)
참고 : https://3months.tistory.com/436, https://yonsodev.tistory.com/7
👇 수식을 이용해 손실 함수로서의 교차 엔트로피를 구현
$cost(W) = - \frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{C} q(x_j)log_2(p(x_j))$
$q(x_j)*-log_2(p(x_j))$ : 텐서 연산이므로 형식 그대로 작성
$\sum_{j=1}^{C}$ : sum으로 구현
$\frac{1}{n} \sum_{i=1}^{n}$ : mean으로 구현
cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()소프트맥스 회귀 실습

1) 입력 X에 가중치 W를 곱하고 b를 더하여 소프트맥스 함수에 입력
2) 소프트맥스 함수는 확률 벡터를 반환
3) 2에서 반환된 확률 벡터와 원-핫 인코딩 된 라벨의 오차를 계산 (손실 함수로 교차 엔트로피 이용)
4) 3에서 계산된 오차로부터 W와 b를 업데이트
👇 본격적으로 소프트맥스 회귀를 구현하기 전에 필요 라이브러리를 임포트, 데이터 준비한다.
# 임포트
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
# 데이터 로드
x_train = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
# one hot encoding
y_one_hot = torch.zeros(8, 3)
y_one_hot.scatter_(1, y_train.unsqueeze(1), 1) # y_train 자리에 1을 scatter
# W,b 초기화
W = torch.zeros((4, 3), requires_grad=True) # X = 8x4, Y = 8x3 이므로 W = 4x3 이여야함
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)👇 소프트맥스 회귀를 구현한다.
파이 토치에서는 Wx+b를 소프트맥스 함수에 입력하고, 교차 엔트로피를 구하는 과정을 한 줄로 나타내는 F.cross_entropy() 함수를 제공한다.
z = x_train.matmul(W) + b, cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean() 수식을 cost = F.cross_entropy(z, y_train) 한 줄로 나타낼 수 있다.
# W,b 최적화
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Wx+b를 소프트맥스에 입력
# z = x_train.matmul(W) + b
hypothesis = F.softmax(z, dim=1) # hypothesis는 예측값 확률벡터
# 교차 엔트로피로 오차 계산
# cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
cost = F.cross_entropy(z, y_train)
# 오차로부터 W,b 업데이트
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
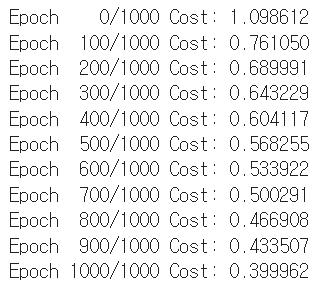
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
실습 링크 : Pytorch/Ch5-1_5 소프트맥스 회귀.ipynb at main · nayonsoso/Pytorch (github.com)
참고 : https://wikidocs.net/59678
'ML' 카테고리의 다른 글
| [ML] 타이타닉 생존자 예측하기 (0) | 2022.01.30 |
|---|---|
| [ML] CNN (0) | 2022.01.23 |
| [ML] 특성 공학과 규제 (1) | 2021.11.05 |
| [ML] 선형 회귀 (0) | 2021.11.04 |
| [ML] K-최근접 이웃 회귀 (0) | 2021.11.04 |

